Problem Statement
Transformer-based[1] Language models have a context length limitation during training. Let’s denote this length as L. It is used to sample L tokens from the training dataset for each training example. As you can imagine, the larger the L, the more compute is needed for training and the slower the training speed. The below figure is from the paper [2]
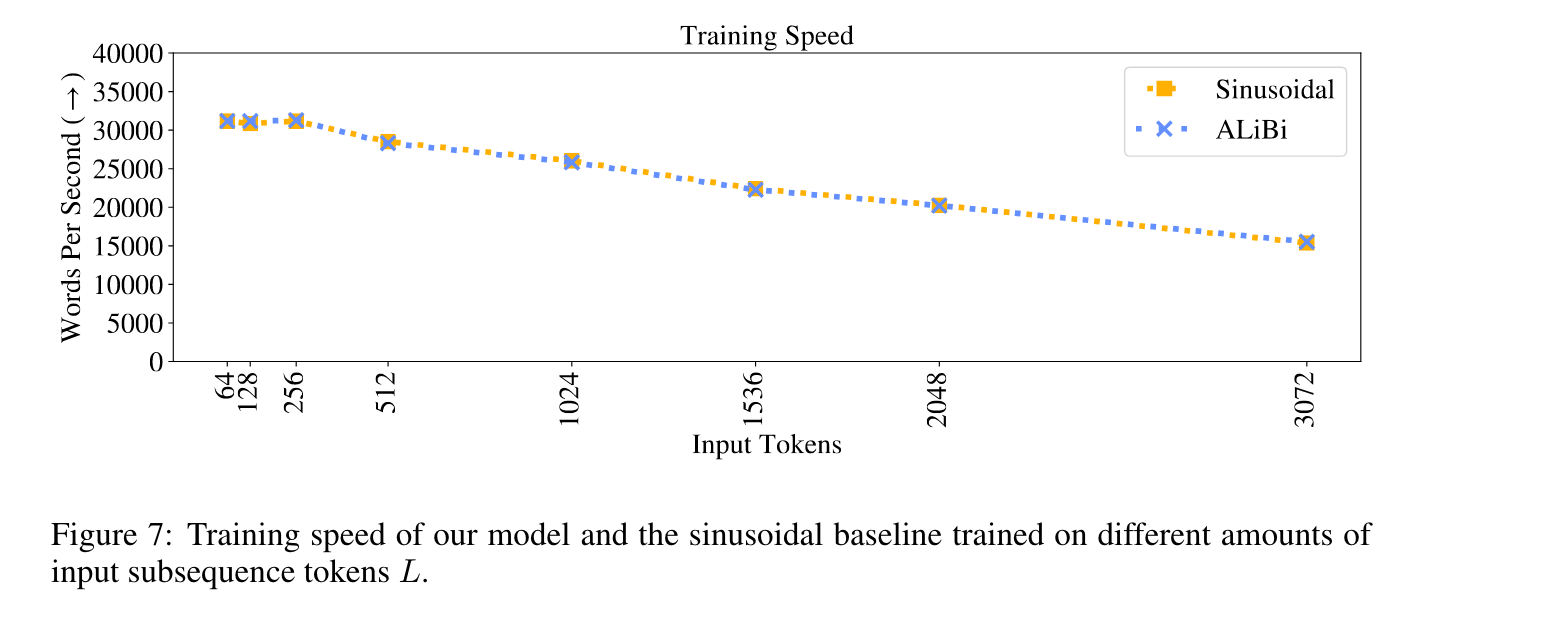
But in inference time, it would be great if the model’s context length can be longer than the training context length. For example, in DeepSeek V2[3], the training context length is 4096. But in real-world applications, the user always want to input more tokens to the model and expect the model to give a response based on the whole conversation history.
So how’s model performance when the number of tokens generated in inference is longer than the training context length? Paper[4] provided some insights on this topic. The below figure showed that when the inference length is longer than the training context length, the model performance will drop dramatically.
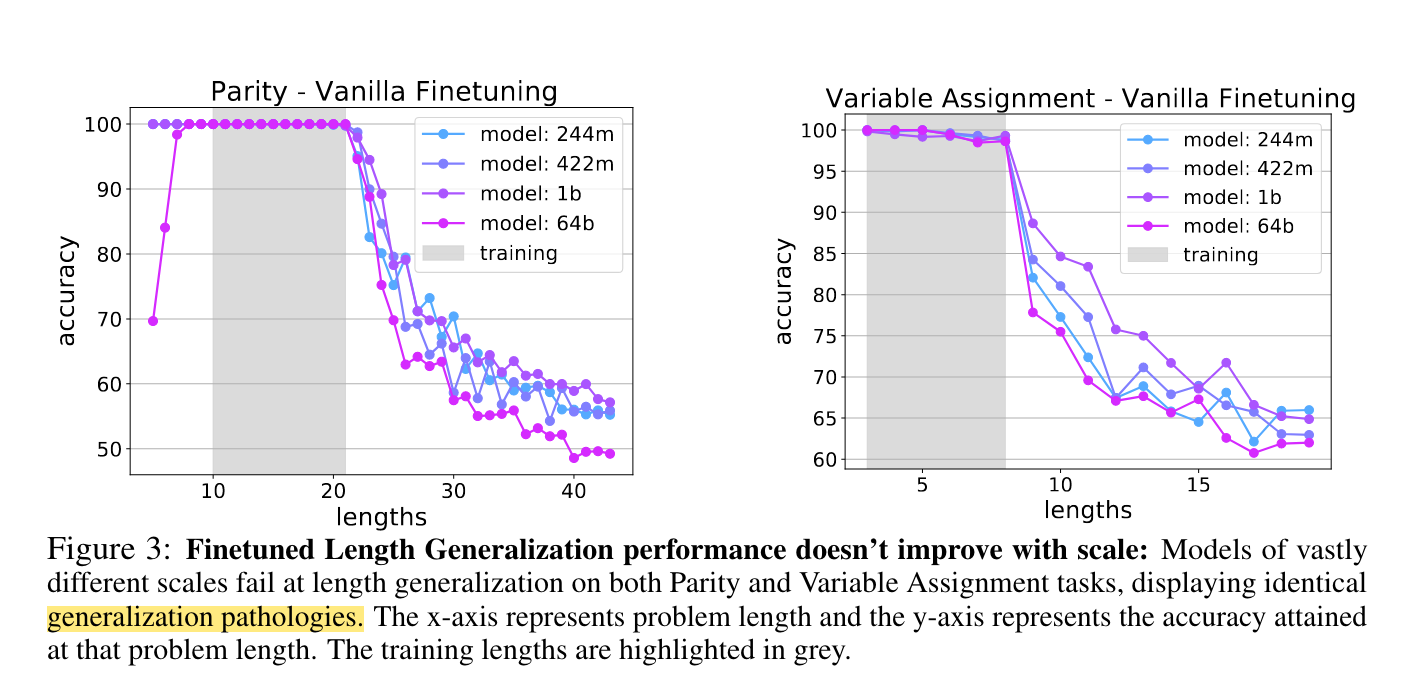
Why does this happen? [2] mentioned that
We demonstrate that this failure to extrapolate is caused by the position embedding method
The extrapolation here means
a model’s ability to continue performing well as the number of input tokens during validation increases beyond the number of tokens on which the the model was trained.
In the following sections, we will talk about how to improve the extrapolation ability of the model.
ALiBi[2]
This is a really great paper, not only for they proposed a method to improve the extrapolation, but also they have a lot of details on the experiment they did and the results they got. As mentioned above, the failure to extrapolate is caused by the position embedding method. So the authors proposed that why not we just remove the position embedding?
ALiBi has an inductive bias towards recency; it penalizes attention scores between distant query-key pairs, with the penalty increasing as the distance between a key and a query grows. The different heads increase their penalties at different rates, depending on the slope magnitude.

I think the key insight here is that the relative position between tokens matters, not the absoluate position of the tokens. With the experiment, the bias toward recency can lead to better extrapolation.
The extrapolation performance of ALiBi is shown in the below figure.
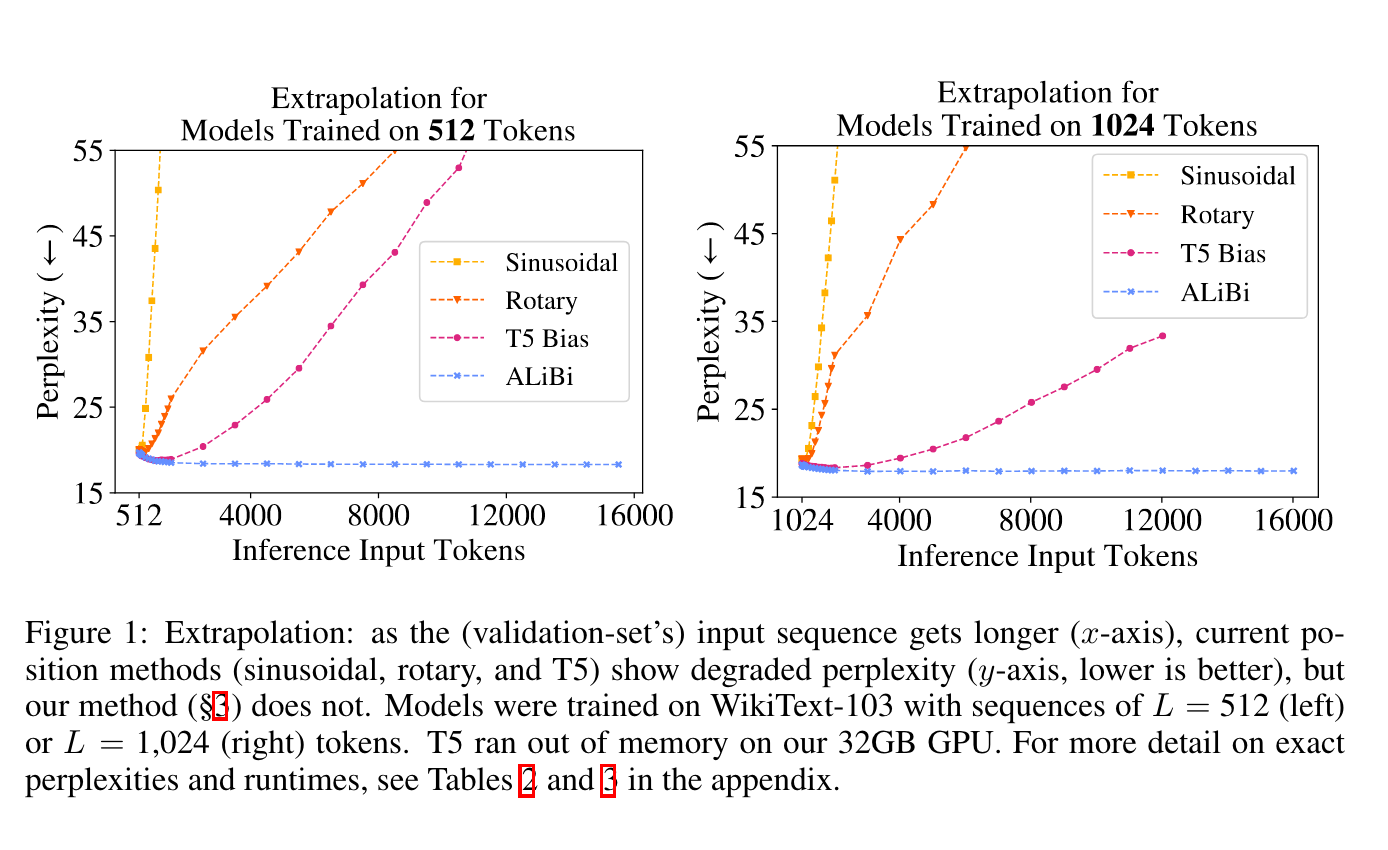
A key limitation of ALiBi is that it is hard to fine-tune the model as the position penalty is added in the pretraining. And many open source models are using some kind of position embedding.
Randomized Positional Embedding[5]
This is actually a very interesting idea. The authors demonstrate that
In this work, we demonstrate that this failure mode is linked to positional encodings being out-of-distribution for longer sequences (even for relative encodings)
So in this paper, the authors proposed that how about eliminating the out of distribution(OOD) position embedding by including them in the training? Wait, does that mean increase the training context length? Actually not, they increase the range of position embedding but still keep the small number of training context length by randomizing selecting the position embeddings during training. One of the key insight here is that the actual position embedding is not important, what matters is the order of the position embeddings. This idea is also some form of ALiBi.

For this method, a relatively large maximum context length L is preset. And during training, N(training context length) random numbers are selected from the range of [0, L-1] and the corresponding position embeddings are used. So the model doesn’t learn a fixed position embeddings for each position. During inference, when inference length is longer than the training context length, the position embeddings are NOT OOD anymore.
The limitation of this method as the author mentioned
The main limitation of our approach is that the maximum test sequence length M has to be known in advance to choose L ≫ M .
However, note that if L is chosen to be much larger than N or M , it is theoretically unlikely for the model to encounter enough unique indices during training, likely leading to poor performance (both in- and out-of-distribution).
Log(N)[6]
The Log(N) method is briefly mentioned in the paper[6]. The authors found that when multiplied the attention score by a factor of log(N), the model can achieve better extrapolation performance. The authors didn’t provide many theorical analysis on why this works. But we will see later in RaRN, they include this idea into their implementation and achieve good extrapolation performance.
Rotary Positional Embedding[7] related content length extension
In this section, we will mainly talk about a few methods to extend the context length for the models that using the RoPE[7] as positional embedding. In the original Transformer paper[1], the positional embeddings are added to the token embeddings at the bottom of the model. RoPE proposed another way to do the position embedding where the query and key are multiplied by a rotation matrix. The $R$ matrix is the rotation matrix and $W_q x_m$ and $W_k x_m$ are the query and key for the $m$-th token.
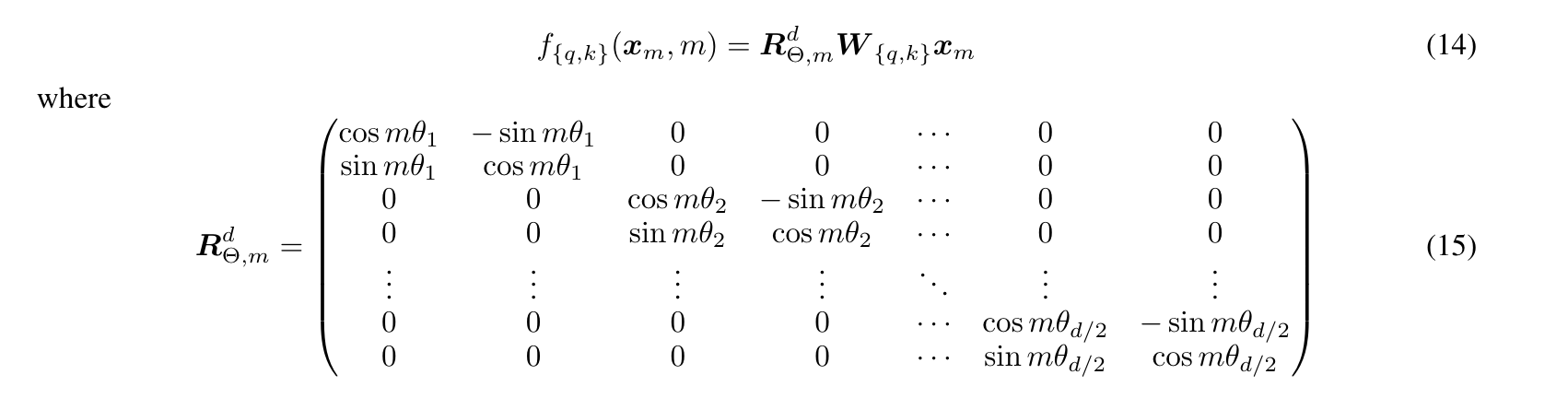
In the following section, I will talk some papers about extending the context length for RoPE. But before that, I just want to say that they improve the extrapolation because they let the position embeddings for the tokens outside the training context length fall into the training context length to some extent. In this way, the OOD position embeddings are not that OOD anymore. Without further ado, let’s get started.
Position Interpolation[8][9]
This work was first proposed by /u/kaiokendev on Reddit[9]. The idea is very simple, but it is difficult to first propose this idea. kaiokendev mentioned that it took a few months experimentation to find this idea actually works. Researchers from Meta had a concurrent work[8]. So for RoPE, each item in the rotation matrix is like $sin(\theta)$ or $cos(\theta)$.
\[\theta = m * b^{-2d / D}\]where $b$ is the base, $m$ is the position index, $d$ is the positional embedding dimension, and $D$ is the size of the positional embedding.
You can see for the OOD position embedding, $m$ is larger than the training context length and that is why it becomes OOD when the inference length is longer than the training context length, since during training, the model never see such position embeddings. For the Positional Interpolation, if we want to increase the inference length as for example 4X of the training context length, then each $m$ becomes $\frac{m}{4}$. In this way, there would be no OOD position index. This one line code change actually works well. As mentioned in the paper[8],
We present Position Interpolation (PI) that extends the context window sizes of RoPE-based (Su et al., 2021) pretrained LLMs such as LLaMA (Touvron et al., 2023) models to up to 32768 with minimal fine-tuning (within 1000 steps), while demonstrating strong empirical results on various tasks that require long context
The limitation are
- fine-tuning is needed to get the extrapolation work.
- For low dimension $d$, after scaling with $\frac{1}{m}$, the adjacent embedding values are closer to each other, thus making it difficult to distinguish the position of the tokens. For example when $d=0$, $\theta = m$. Before the scaling, the adjacent embedding difference would be 1, but now the difference is $\frac{1}{m}$.
NTK-Aware[10]
Very interestingly, this idea was also first proposed on Reddit by /u/bloc97. bloc97 was inspired by kaiokendev and pointed out that the interpolation by scaling $m$ is suboptimal from the Neural Tangent Kernel(NTK) perspective. Really amazing insight! bloc97 proposed to change base instead of scaling $m$. Specifically, the change is
\[\theta = m * {b'}^{\frac{-2d}{D}}\]and
\[b' = b * {\alpha}^{\frac{D}{D-2}}\]where $\alpha$ is the scaling factor. Since $\alpha > 1$ and ${\frac{D}{D-2}} > 1$, the new base $b’$ is larger than the original base $b$.
You may wonder why this works? I had the same question when I first read the post. But if you take a look at $\theta = m * b^{-2d / D}$ again, you will find that increasing $b$ has similar effect as decreasing $m$ which is what Position Interpolation did. So the idea is similar that making the inference position embeddings fall into the training position embeddings range. But the difference between Position Interpolation and NTK-Aware is that due to the exponent ${-\frac{2d}{D}}$, the effect of increasing $b$ is non-linear.
What is amazing is that as mentioned in [10], it can achieve similar extrapolation performance as Position Interpolation without fine-tuning.
One thing I want to highlight here is that for low dimension $d$, for example when $d=0$, $\theta = m$, the NTK-Aware is actually a pure extrapolation method. So you can see NTK-Aware as a method that for low dimension $d$, it is extrapolation, for high dimension $d$, it is interpolation.
You may also wonder why $b’ = b * {\alpha}^{\frac{D}{D-2}}$? $\alpha$ is actually the scaling factor, when $\alpha = 4$, roughly speaking, it will help extend the context length to 4X of the training context length. But where does that $\frac{D}{D-2}$ come from? From [11], the new base $b’$ can be chosen so that
\[b'^{\frac{D-2}{D}} = \alpha * b ^{\frac{D-2}{D}}\]It just makes the last dimension $d$ the base change is the same as the Position Interpolation.
YaRN[11]
The primary author of YaRN[11] is actually the reddit users /u/bloc97. It proposed another NTK related method called NTK-by-Parts combined with Log(N) method we mentioned above. The authors mentioned a disadvange of NTK-Aware[10] is that
However, one major disadvantage of this method is that given it is not just an interpolation scheme, some dimensions are slightly extrapolated to “out-of-bound” values, thus fine-tuning with “NTK-aware” interpolation [6] yields inferior results to PI [9].
It is not difficult to understand what it means, since we mentioned this with an example above.
To improve on this, they proposed a method called NTK-by-Parts. They think about this from the perspective of wavelength. The wavelength of a sinusoidal function here is $2*\pi * b^{2d / D}$. Since the sinusoidal function is periodic, the wavelength can be described as how many tokens away, they will have the same $cos$ or $sin$ values. For some dimension $d$, the wavelength is larger than the training context length, in this case, the extrapolation is not working well as the model doesn’t see those position embeddings during training. So they proposed in this case, the interpolation should be used. But for $d$ whose wavelengths are very small, interpolation should not be used. In other words, extrapolation should be used. When in between, both interpolation and extrapolation should be used.
Also they incorporate the idea of Log(N), but not directly apply it to the attention score. Instead, they apply it to the position embedding so that when fine-tuning, only the position embedding needs to be changed.
The experiment shows that YaRN is much more efficient than PI
We show that YaRN successfully achieves context window extension of language models using RoPE as its position embedding. Moreover, this result is achieved with only 400 training steps, representing approximately 0.1% of the model’s original pre-training corpus, a 10x reduction from Rozière et al. [31] and 2.5x reduction in training steps from Chen et al. [9], making it highly compute-efficient for training with no additional inference costs.
where Chen et al. [9] is the Position Interpolation method.
Finally, I just want to cite how DeepSeek V2[3] uses YaRN to extend the context length,
After the initial pre-training of DeepSeek-V2, we employ YaRN (Peng et al., 2023) to extend the default context window length from 4K to 128K. YaRN was specifically applied to the decoupled shared key kR t as it is responsible for carrying RoPE (Su et al., 2024). For YaRN, we set the scale s to 40, α to 1, β to 32, and the target maximum context length to 160K. Under these settings, we can expect the model to respond well for a context length of 128K. Slightly diverging from original YaRN, due to our distinct attention mechanism, we adjust the length scaling factor to modulate the attention entropy. The factor √ t is computed as √ t = 0.0707 ln s + 1, aiming at minimizing the perplexity. We additionally train the model for 1000 steps, with a sequence length of 32K and a batch size of 576 sequences. Although the training is conducted solely at the sequence length of 32K, the model still demonstrates robust performance when being evaluated at a context length of 128K. As shown in Figure 4, the results on the “Needle In A Haystack” (NIAH) tests indicate that DeepSeek-V2 performs well across all context window lengths up to 128K.
References
[1]: A. Vaswani, N. Shazeer, N. Parmar, J. Uszkoreit, L. Jones, A. N. Gomez, L. Kaiser, and I. Polosukhin. Attention is all you need. In Advances in Neural Information Processing Systems, volume 30. Curran Associates, Inc., 2017.
[2]: O. Press, N. Smith, and M. Lewis. Train Short, Test Long: Attention with linear biases enables input length extrapolation. In International Conference on Learning Representations, 2022.
[3]: DeepSeek-V2: A Strong, Economical, and Efficient Mixture-of-Experts Language Model, 2024.
[4]: @misc{anil2022exploringlengthgeneralizationlarge, title={Exploring Length Generalization in Large Language Models}, author={Cem Anil and Yuhuai Wu and Anders Andreassen and Aitor Lewkowycz and Vedant Misra and Vinay Ramasesh and Ambrose Slone and Guy Gur-Ari and Ethan Dyer and Behnam Neyshabur}, year={2022}, eprint={2207.04901}, archivePrefix={arXiv}, primaryClass={cs.CL}, url={https://arxiv.org/abs/2207.04901}, }
[5]: @misc{ruoss2023randomizedpositionalencodingsboost, title={Randomized Positional Encodings Boost Length Generalization of Transformers}, author={Anian Ruoss and Grégoire Delétang and Tim Genewein and Jordi Grau-Moya and Róbert Csordás and Mehdi Bennani and Shane Legg and Joel Veness}, year={2023}, eprint={2305.16843}, archivePrefix={arXiv}, primaryClass={cs.LG}, url={https://arxiv.org/abs/2305.16843}, }
[6]: @misc{chiang2022overcomingtheoreticallimitationselfattention, title={Overcoming a Theoretical Limitation of Self-Attention}, author={David Chiang and Peter Cholak}, year={2022}, eprint={2202.12172}, archivePrefix={arXiv}, primaryClass={cs.LG}, url={https://arxiv.org/abs/2202.12172}, }
[7]: @misc{su2023roformerenhancedtransformerrotary, title={RoFormer: Enhanced Transformer with Rotary Position Embedding}, author={Jianlin Su and Yu Lu and Shengfeng Pan and Ahmed Murtadha and Bo Wen and Yunfeng Liu}, year={2023}, eprint={2104.09864}, archivePrefix={arXiv}, primaryClass={cs.CL}, url={https://arxiv.org/abs/2104.09864}, }
[8]: @misc{chen2023extendingcontextwindowlarge, title={Extending Context Window of Large Language Models via Positional Interpolation}, author={Shouyuan Chen and Sherman Wong and Liangjian Chen and Yuandong Tian}, year={2023}, eprint={2306.15595}, archivePrefix={arXiv}, primaryClass={cs.CL}, url={https://arxiv.org/abs/2306.15595}, }
[9]: https://www.reddit.com/r/LocalLLaMA/comments/14fgjqj/a_simple_way_to_extending_context_to_8k/
[10]: https://www.reddit.com/r/LocalLLaMA/comments/14lz7j5/ntkaware_scaled_rope_allows_llama_models_to_have/
[11]: @misc{peng2023yarnefficientcontextwindow, title={YaRN: Efficient Context Window Extension of Large Language Models}, author={Bowen Peng and Jeffrey Quesnelle and Honglu Fan and Enrico Shippole}, year={2023}, eprint={2309.00071}, archivePrefix={arXiv}, primaryClass={cs.CL}, url={https://arxiv.org/abs/2309.00071}, }