Flash Attention

The full Numpy implementation code could be found at my github repo fastAttention.

Flash Attention is a faster way to compute attention operation. For what attention is, please refer to the Transformer paper Attention is All You Need. Flash Attention is building on top of a 2018 paper Online normalizer calculation for softmax which discussed about how to compute softmax in online fashion to reduce the number of memory access between Chip and Memory. For GPU, it is between Chip SRAM and High Bandwidth Memory (HBM).

Online normalizer calculation for softmax

Tranditionally to compute softmax for a vector of values, we will first load the values from memory, compute the sum of exponential. Then load the values again and divide the exponential ofeach value by the sum of exponential computed in the first step. Finally load the resutls back to memory. So totally we have 3 memory access, two loads and one store. The code in Python is like

def standard_softmax(x):
    total = 0
    # first load each element to get the sum of the exponential
    for v in x:
        total += math.exp(v)
    # second load each element to get the result
    res = []
    # one store operation
    for v in x:
        res.append(math.exp(v) / total)
    return res

Safe softmax

The drawback of the above implementation is that it is not numerical stable because we calculate the exponential and sum them together. When the input values are large, the exponential will be very large and the sum will overflow. To fix this, we could get the max value of the input and then subtract it from each value. This way the exponential will be smaller and the sum will be less like to overflow. The code is like

def safe_softmax(x):
    max_value = float('-inf')
    # first load each element to find the max value
    for v in x:
        if v > max_value:
            max_value = v
    total = 0.0
    # second load each element to calculate the sum of the exponential
    for v in x:
        total += math.exp(v - max_value)
    # third load each element to calculate the result
    res = []
    # one store operation
    for v in x:
        res.append(math.exp(v - max_value) / total)
    return res

This will need 4 memory access, three loads and one store.

Online softmax

Fewer memory access will improve the performance of calculating softmax, so the authoers proposed a new way which they called online softmax. The key insights from the authors are

  1. To get max, we just need to read a new value and compare with the existing max
  2. To update the sum, just need multiply exp(old_max) and then divide by exp(new_max)

So we can compute the max and sum in a single pass incrementally. In Flash Attention, the exactly same idea will be used to compute the softmax only for a block of 2 dimensional matrix instead of a single vector.

def online_softmax(x):
    total = 0.0
    max_value = float('-inf')
    # first load each element to find the max value and sum of the exponential
    for v in x:
        old_max = max_value
        if v > max_value:
            max_value = v
        total = total * math.exp(old_max - max_value) + math.exp(v - max_value)
    # second load each element to calculate the result
    res = []
    # one store operation
    for v in x:
        res.append(math.exp(v - max_value) / total)
    return res

As we can see, it will need 3 memory access, two loads and one store.

Flash Attention

So why softmax matters here when we are talking about Flash Attention? Because softmax is a key part of the attention. You can see how online softmax can reduce the memory access, this will also help attention to reduce the memory access to improve the performance.

Attention

Just a brief introdution of attention. We have 3 matrices, Q, K and V. For simplcity, we assume the dimensions of them are the same, N by d.

Attention is as follows, and the multiplication here is matrix multiplication.

  1. Q * K^T will get a N by N matrix, which is the similarity between each query and key.
  2. softmax(Q * K^T) will get a N by N matrix, which is the attention score. Note that softmax is applied row-wise and it is safe softmax.
  3. attention_score * V will get a N by d matrix, which is the attention output.

Matrix multiplication block by block

If the matrices are not very small, usually we need to compute the matrix multiplication block by block. What does that mean? For Q, we will divide it into N/b_r blocks where each block is of size b_r by d. For K, we will divide it into N/b_c blocks where each block is of size b_c by d. For V, we will divide it into N/b_c blocks where each block is of size b_c by d. So for each matrix, if you stack the blocks vertically you will get the original matrix.

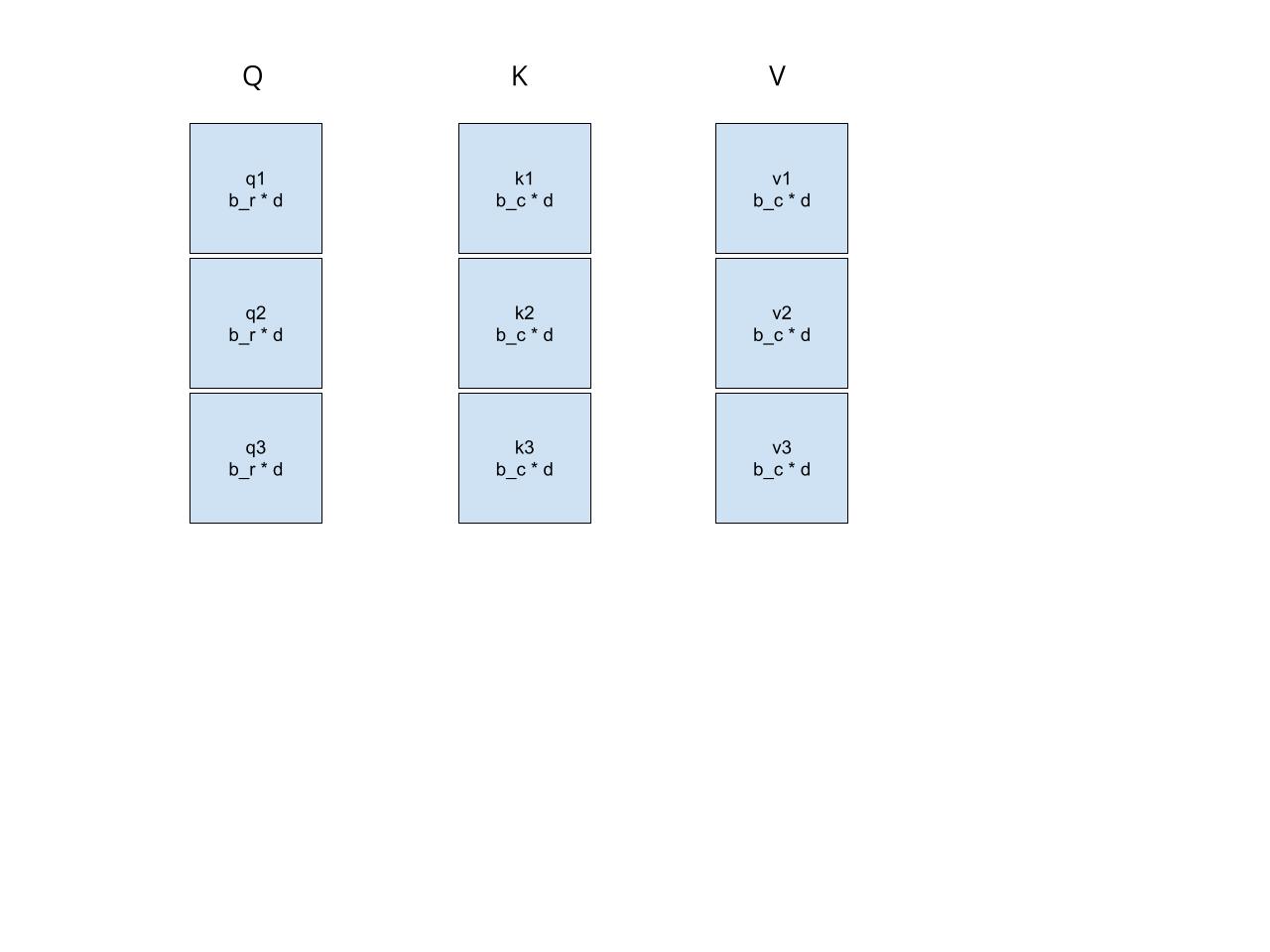
block q k v

Let’s calculate $Q * K^T$ block by block.

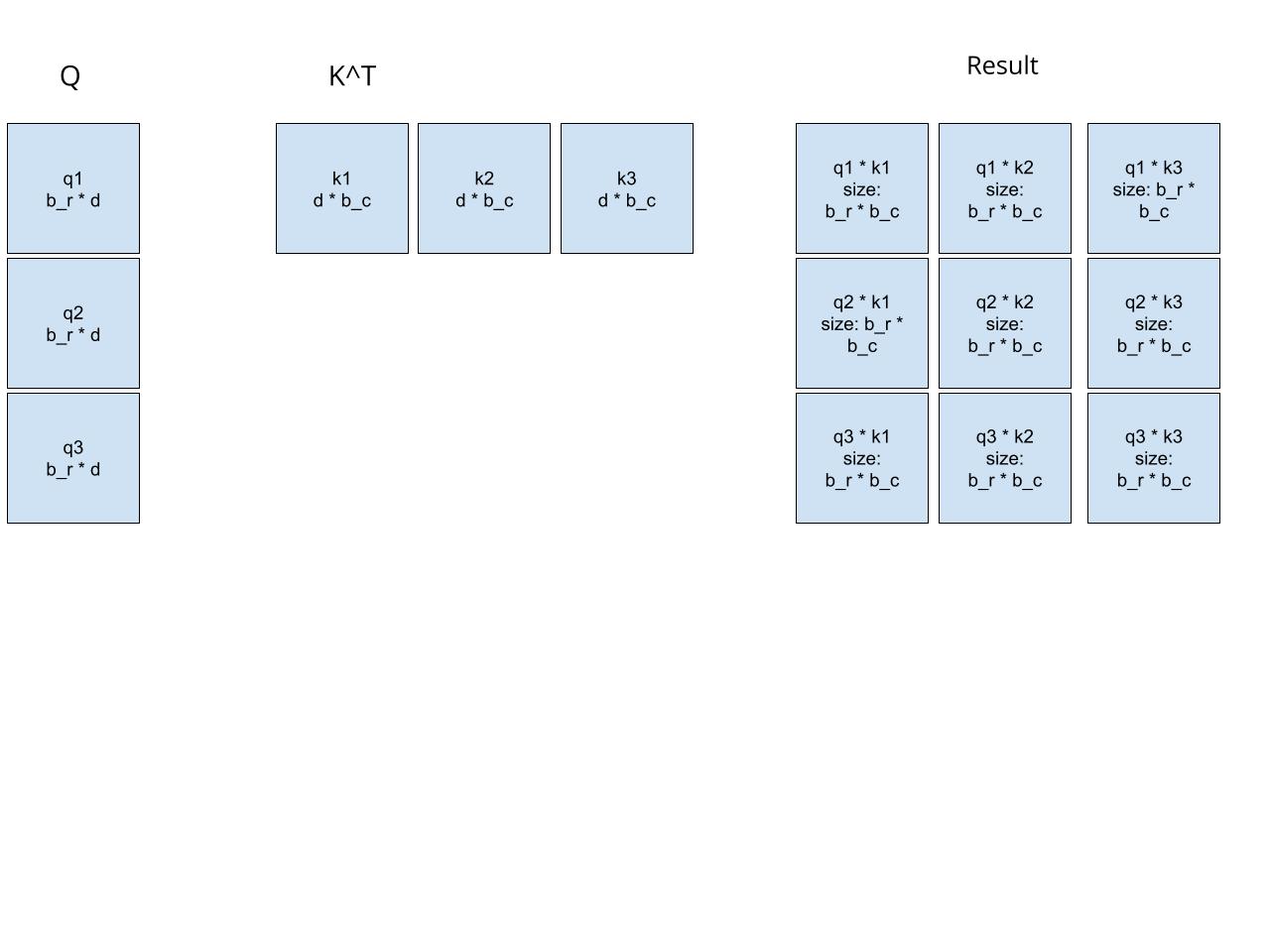
q time k

Let’s ignore softmax for now. And use the results above to do matrix multiplication with v.

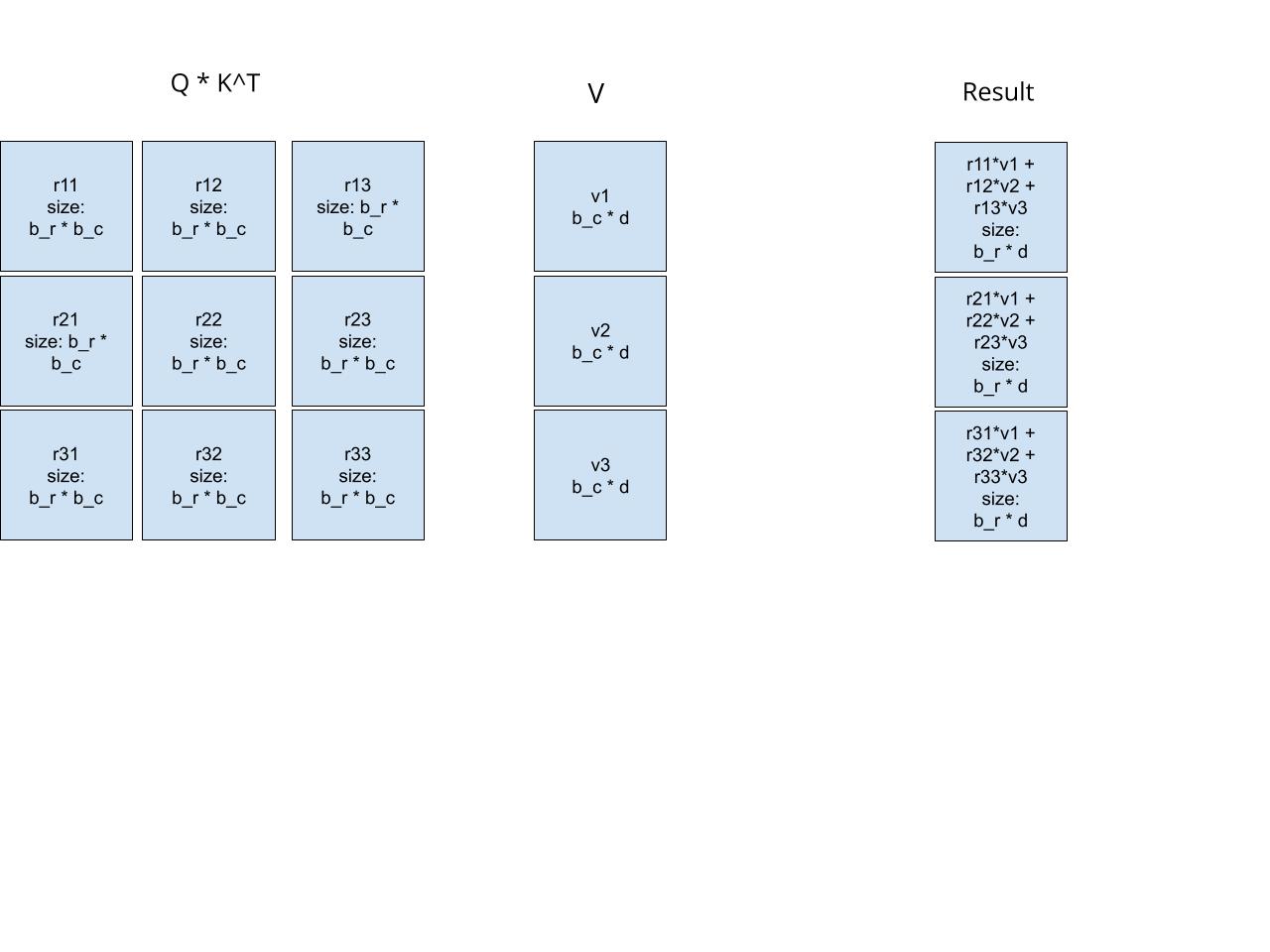
q time k time v

The key point here is that the final each block in the final results could be obtained as the sum of 3 block matrix multiplications. So we could get the final results incrementally block by block.

Flash Attention

So we ignore the softmax above, now let’s add softmax to $Q * K^T$. And this is what Flash Attention does. Now we know that we could compute the attention output incrementally block by block, and we also know that we could compute the softmax incrementally by updating the max and sum. With those two insights, Flash Attention could compute the attention output incrementally block by block.

For each block, it maintains a vector for max and sum which represents the corresponding results for each row in the block. The Python code is like below


def flash_attention(q, k, v, b_r, b_c):
    """
    Calculates the attention with flash attention method.
    
    The FLOPs is O(N^2 * d)
    
    The additional memory required is for m and l which is O(N)

    Args:
        q: Query matrix (shape: (N, d))
        k: Key matrix (shape: (N, d))
        v: Value matrix (shape: (N, d))
        b_r: The block size for q
        b_c: The block size for k and v
    Returns:
        attention_output: Output of the attention mechanism (shape: (N, d))
    """
    assert q.shape[0] % b_r == 0, "the number of rows of q must be divisible by b_r"
    assert k.shape[0] % b_c == 0, "the number of rows of k must be divisible by b_c"
    assert v.shape[0] % b_c == 0, "the number of rows of v must be divisible by b_c"
    assert q.shape[1] == k.shape[1] == v.shape[1], "the number of columns of q, k, v must be the same"
    
    # the output of the flash attention
    o = np.zeros_like(q)

    N = q.shape[0]
    # the sum of exponential vector for each row
    l = np.zeros((N, 1))
    # the max value for each row
    m = np.full((N, 1), float('-inf'))
    
    # divide the q into blocks and each block has size b_r * d
    q_blocks = [q[i:i+b_r, :] for i in range(0, N, b_r)]
    # divide the k into blocks and each block has size b_c * d
    k_blocks = [k[i:i+b_c, :] for i in range(0, N, b_c)]
    # divide the v into blocks and each block has size b_c * d
    v_blocks = [v[i:i+b_c, :] for i in range(0, N, b_c)]
    # divide the o into blocks and each block has size b_r * d
    o_blocks = [o[i:i+b_r, :] for i in range(0, N, b_r)]
    # divide the l into blocks and each block has size b_r * 1
    l_blocks = [l[i:i+b_r, :] for i in range(0, N, b_r)]
    # divide the m into blocks and each block has size b_r * 1
    m_blocks = [m[i:i+b_r, :] for i in range(0, N, b_r)]
    
    n_q_blocks = len(q_blocks)
    n_k_blocks = len(k_blocks)
    
    for j in range(n_k_blocks):
        # load k_j and v_j from HBM to on-chip SRAM, line 6
        k_block = k_blocks[j]
        v_block = v_blocks[j]
        # so for FLOPs, the dominant part is b_r * b_c * d, we have n_k_blocks * n_q_blocks * b_r * b_c * d which is O(N^2 * d)
        for i in range(n_q_blocks):
            # load q_i, m_i, l_i, o_i from HBM to on-chip SRAM, line 8
            q_block, m_block, l_block, o_block = q_blocks[i], m_blocks[i], l_blocks[i], o_blocks[i]
            # calculate the dot product of size b_r * b_c, line 9, FLOPs: b_r * b_c * d
            s_i_j = np.matmul(q_block, k_block.T)
            # calculate the max value for each row, b_r * 1, line 10, FLOPs: b_r * d
            m_i_j = np.max(s_i_j, axis=1, keepdims=True)
            # calculate nominator of the softmax of size b_r * b_c, line 10, FLOPs: b_r * b_c * d
            p_i_j = np.exp(s_i_j - m_i_j)
            # calcualte the sum of the exponential for each row, line 10, FLOPs: b_r * d
            l_i_j = np.sum(p_i_j, axis=1, keepdims=True)
            # get the new max value for each row, line 11, FLOPs: b_r * d
            m_i_new = np.maximum(m_block, m_i_j)
            # get the new sum of exponential vector for each row, line 11, FLOPs: 2 * (b_r * d + d)
            l_i_new = l_block * np.exp(m_block - m_i_new) + l_i_j * np.exp(m_i_j - m_i_new)
            # update the output matrix O, line 12, FLOPs: (b_r * b_c * d + b_r * d) + b_r * d + b_r
            current_o_block = np.exp(m_i_j - m_i_new) * p_i_j @ v_block # b_r * d
            updated_old_o_block = l_block * np.exp(m_block - m_i_new) * o_blocks[i] # FLOPs: b_r * d + b_r
            # update output matrix block and store to HBM, line 12, FLOPs: 2 * (b_r * d + b_r)
            o_blocks[i] = (current_o_block + updated_old_o_block) / l_i_new # b_r * d
            # update the max value for each row and store to HBM, line 13, FLOPs: b_r
            m_blocks[i] = m_i_new # b_r * 1
            # update the sum of exponential vector for each row and store to HBM, line 13, FLOPs: b_r
            l_blocks[i] = l_i_new # b_r * 1
            
    o = np.concatenate(o_blocks, axis=0)
    return o

What Flash Attention Tells Us